On a smooth manifold, vector lives in the tangent vector space, while 1-form lives in the cotangent space.

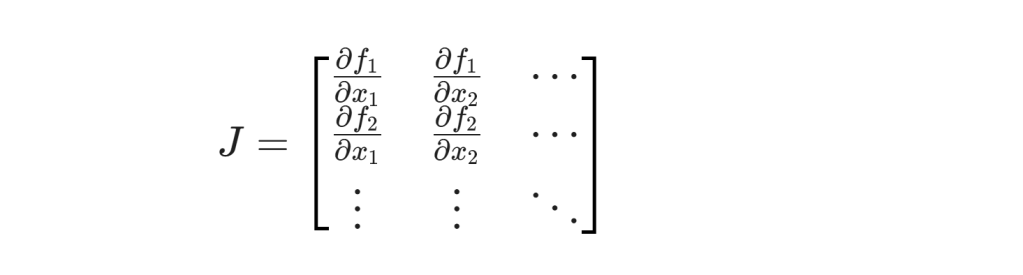
Note lot of confusion comes from the understanding of the basis vector and basis covetor. Vectors transform with Jacobian, 1-forms transform with the inverse transpose Jacobian.

On a non-flat surface (a manifold), basis vectors are no longer fixed constants. Instead, they are local—meaning they change their direction and length depending on exactly where you are standing on that surface.

Then we discuss directional derivative, covariant derivative and exterior derivative! Exterior derivative is totally different than directional or covariant derivative, it acts on differential forms who lives in covector space!

Exterior derivative takes a “measurement” and tells you how it changes as you walk around a tiny loop. it increases degree by 1:

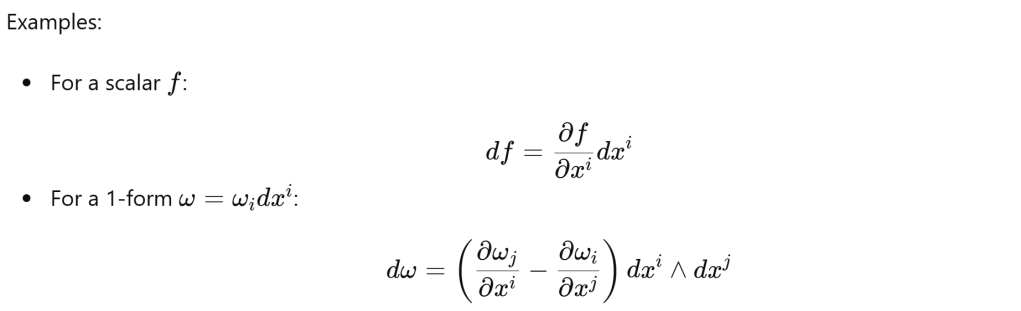
Covariant derivative is extension/comprehensive version of directional derivative, it can work on higher rank vector or tensor. We know directional derivative is the change per unit on one direction, then covariant derivative is the change per unit on a field composed of vectors. curvature, hence Christopher symbol, connection, Levi-Civita connection etc. will need to be considered:

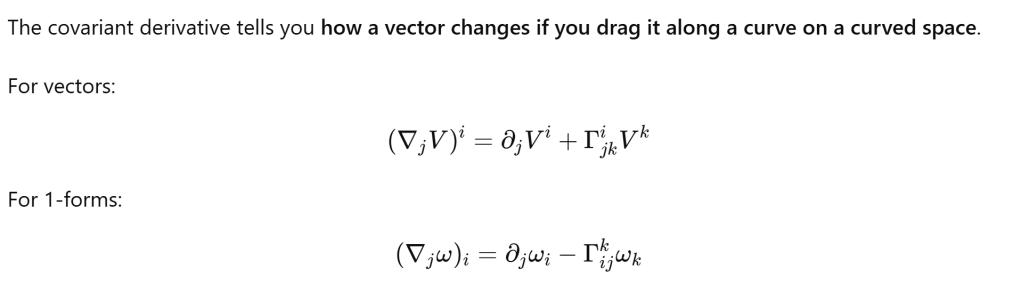
Now move on to the concept of tensor, metric tensor, tensor is defined as multi-linear mapping, basic metric tensor can be derived from this definition

In physics and differential geometry, we often use the metric tensor to measure the distance between two points that are infinitesimally close. This is called the line element $ds^2$. so we can use simple/direct way to deduce metric tensor in non-flat space too.