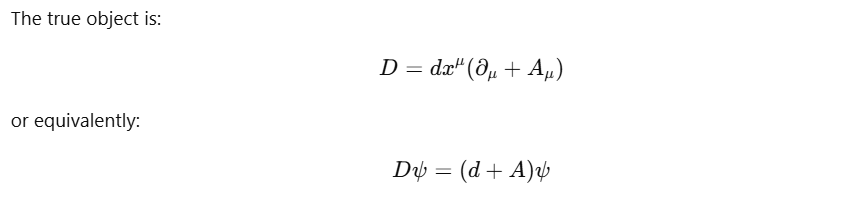Learning math is learning a language, being exact and precise is the key, which requires some efforts to fully understand and practice using them. So one needs to know basis vector, basis covector, their components to achieve math fluency!

d is a map (an operator)! Here is its official definition:

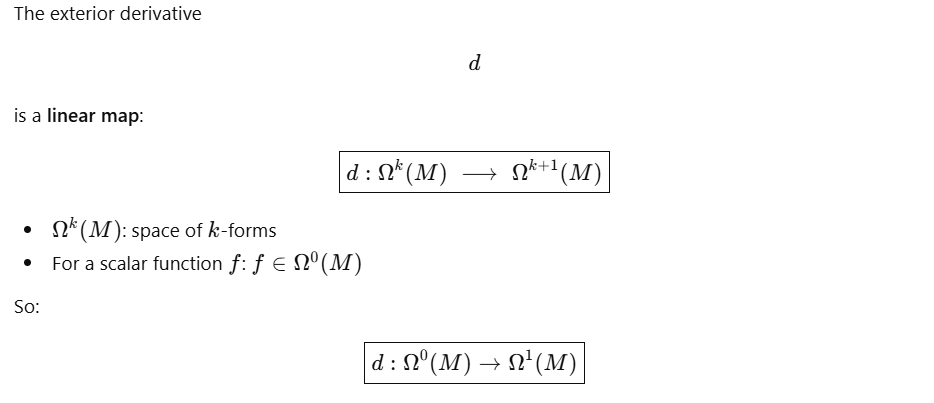
So make it crystal clear that

$$\boxed{ \text{gradient of } f \;\text{is a vector, while } df \;\text{is a covector (1-form).} }$$

Now we can understand what covarient derivative is. The connection is a 1-form; the covariant derivative is the operator that uses it.

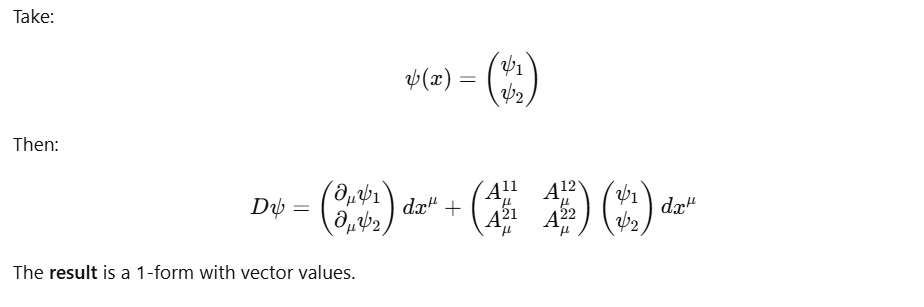
Unfortunately, physicists write equations more sloppy than mathematicians, making it harder for novice learners. D=d + A is accurate, but we often see

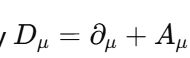
$\partial_\mu$∂μ​ is a basis vector field (derivation); $A_\mu$Aμ​ are components of a 1-form, You cannot literally add them.