We know Lorentz group SO(1,3) in transforming the 4-component space-time vector very well.

A quick recap on how it’s deduced:

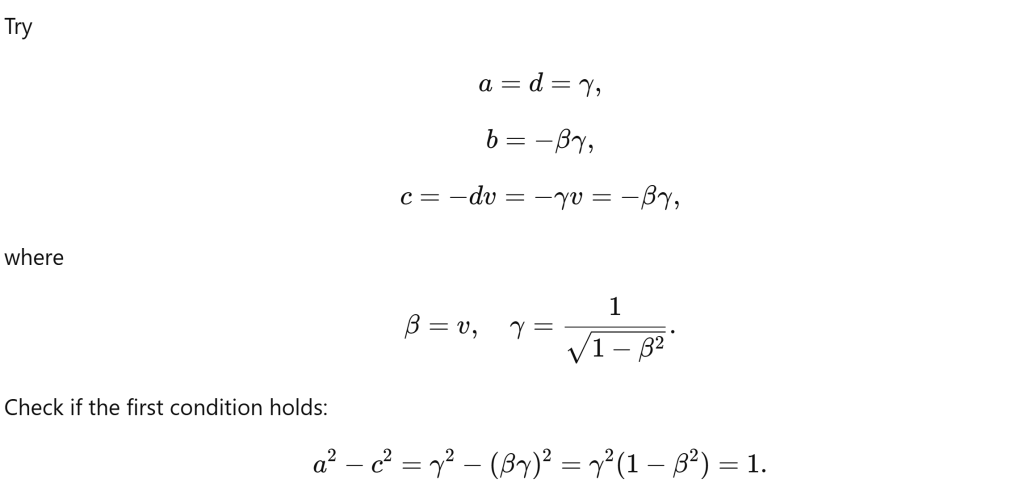
But to describe mathematically spinor, which has “topological twists” and do not respond to 4-vectors, we need something more complex then simple Lorentz transform. We need its double cover SL(2, C).

Chirality is a property of spinors describing their “handedness”: whether they transform as left-handed ($\psi_L$ψL​) or right-handed ($\psi_R$ψR​) under the Lorentz group’s chiral representations. It distinguishes two fundamentally different types of spin-½ particles, especially important for massless fermions and weak interactions.