Penrose said “spinors are the square roots of vectors”, it reveals deep insight of how the nature works.

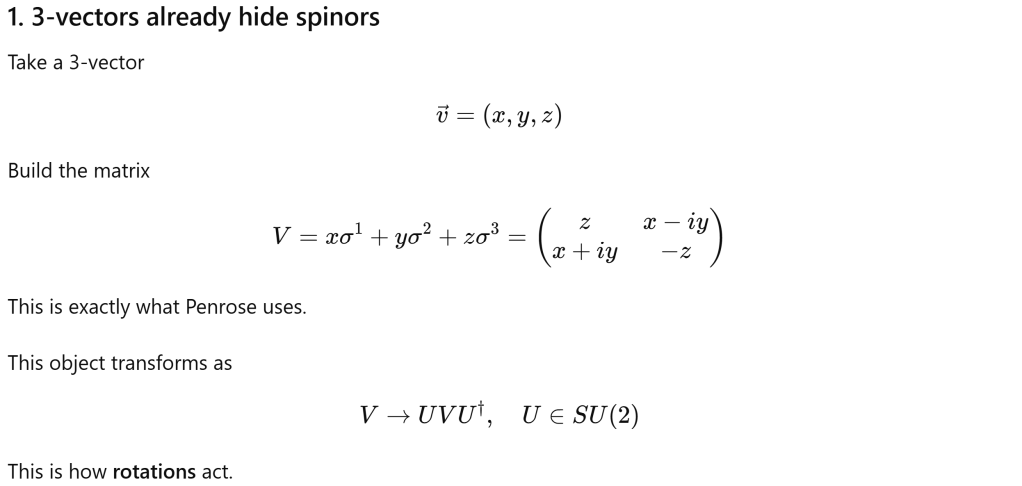
Where we can see a three-component vector can be expressed by 2×2 complex-element matrix.

But the key idea of spinors are square roots of vectors go further:

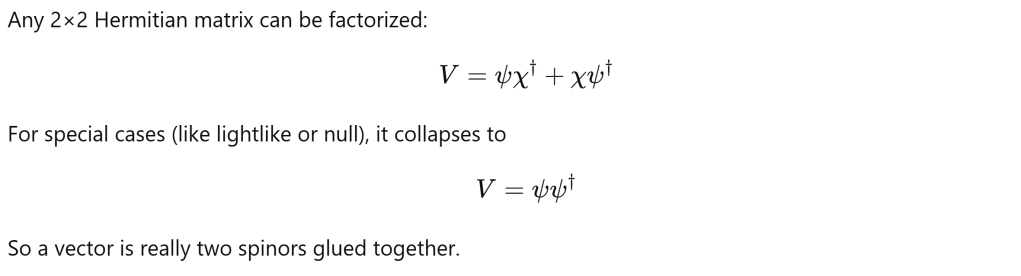
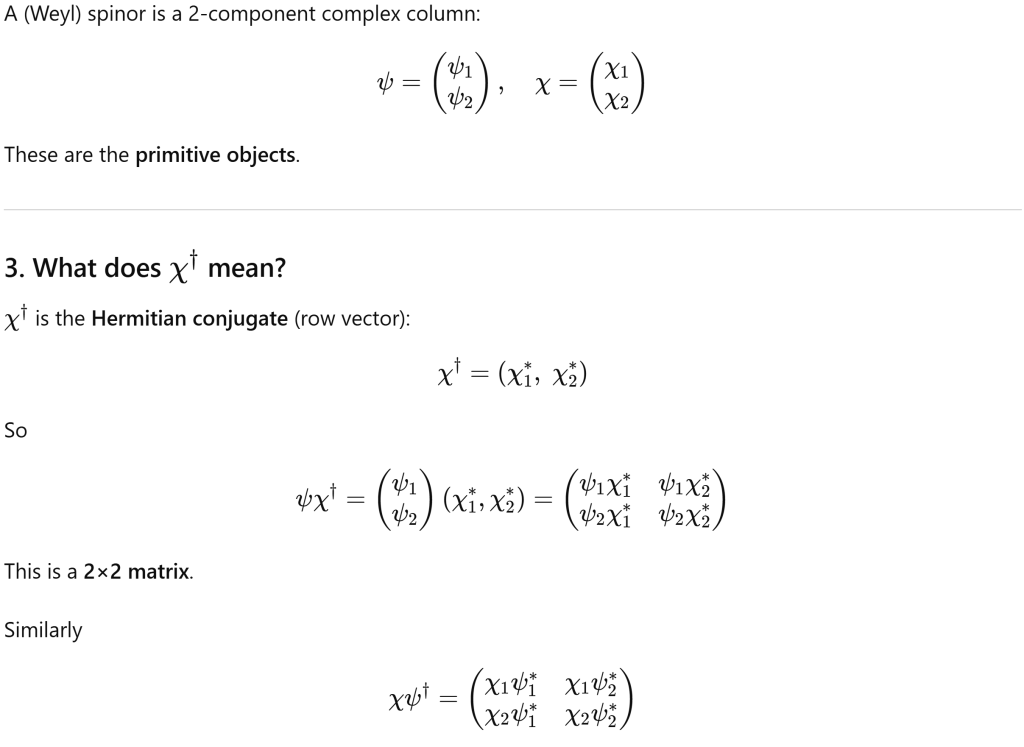
Now illustrate with very concrete example

How to connect the two Weyl spinors just used, $\psi$ψ and $\chi$χ, to$$(\tfrac12,0)\quad\text{and}\quad(0,\tfrac12).$$

Above content blend Pauli spinor and Weyl spinor, Chriseigen has a clear comparison of them

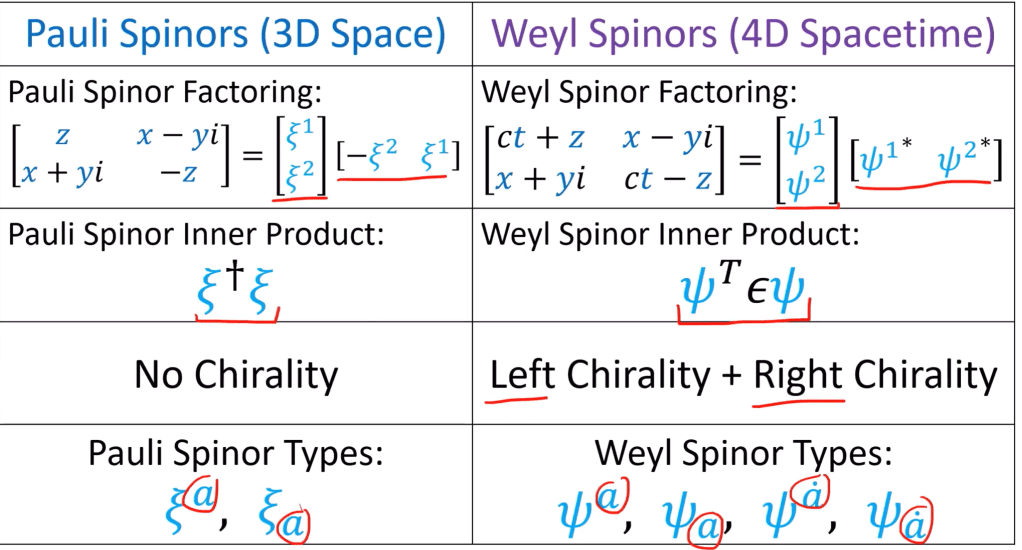
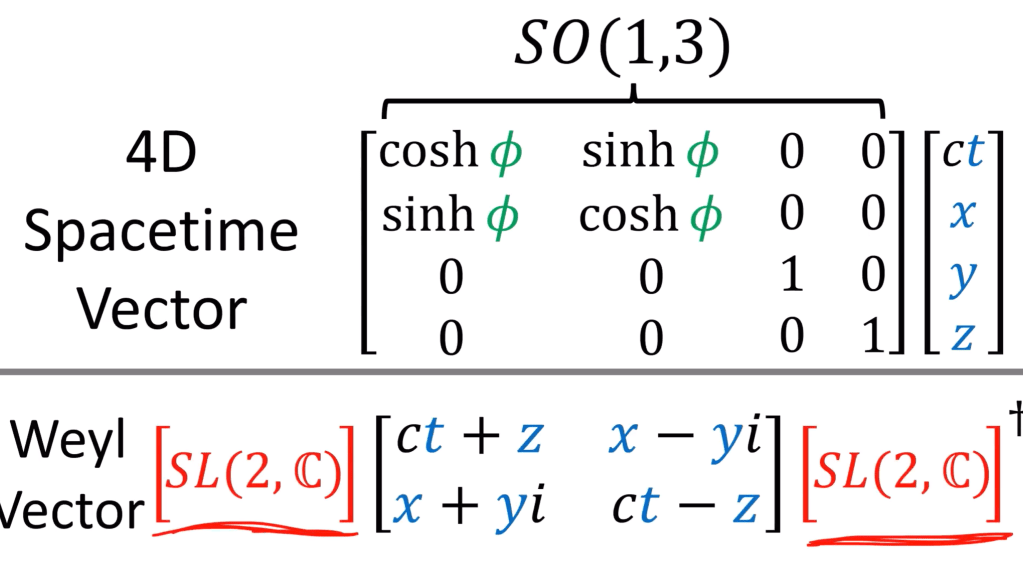
the key here is to rewrite the part in middle to pauli spinor and weyl spinor

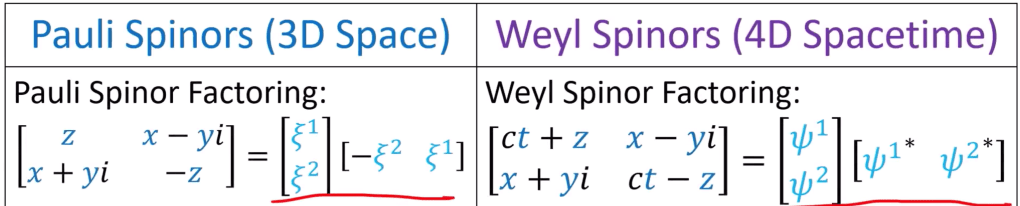
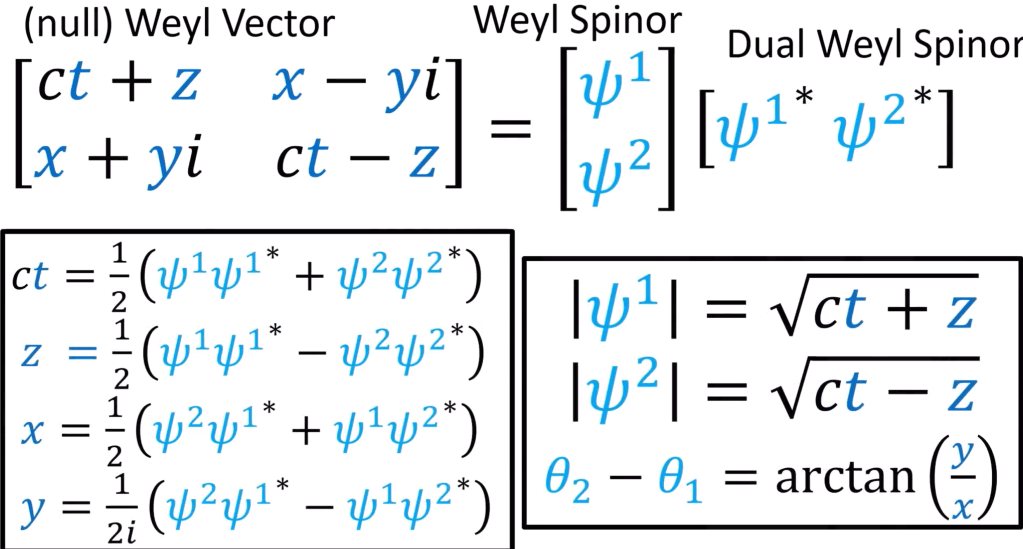
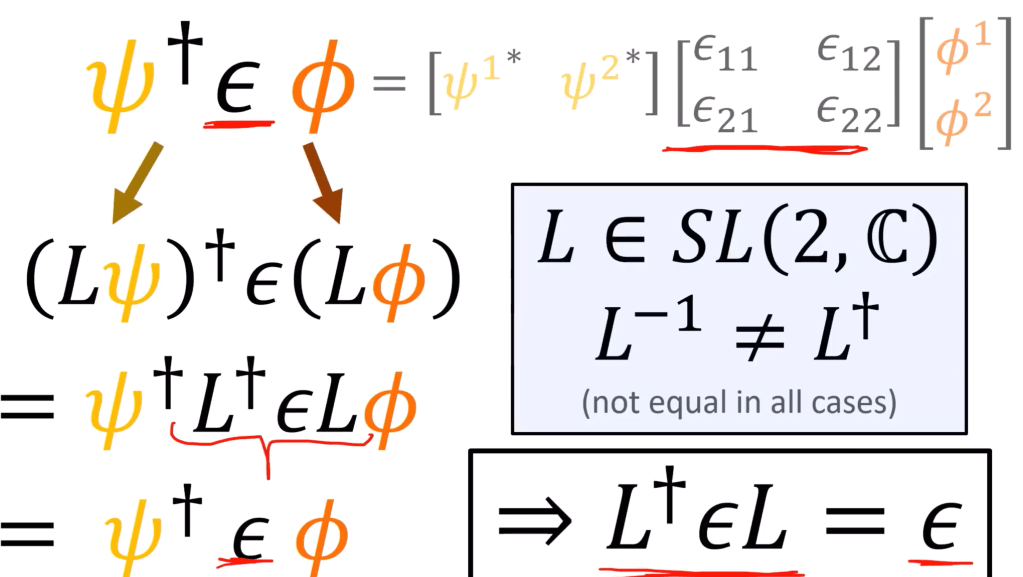
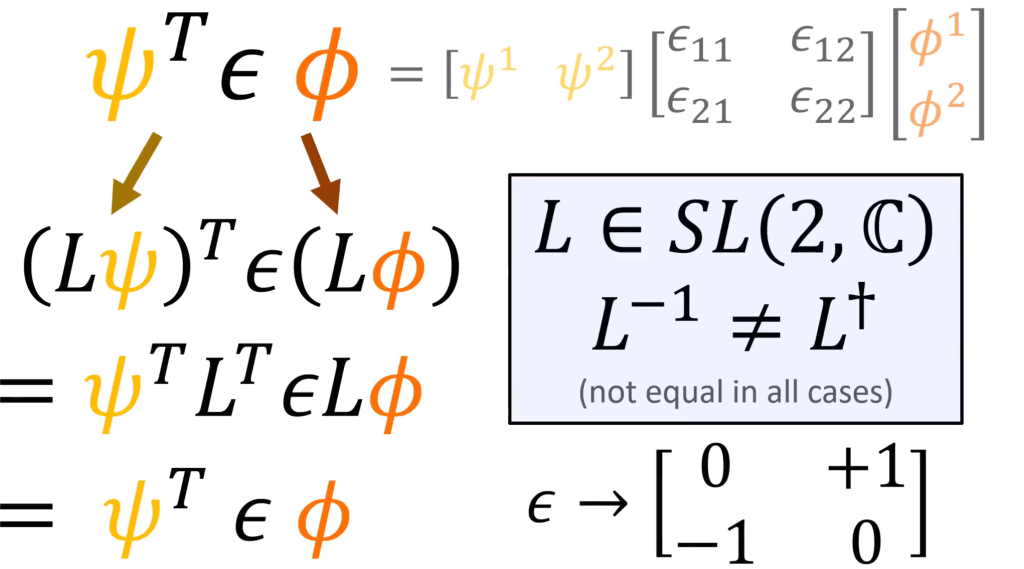
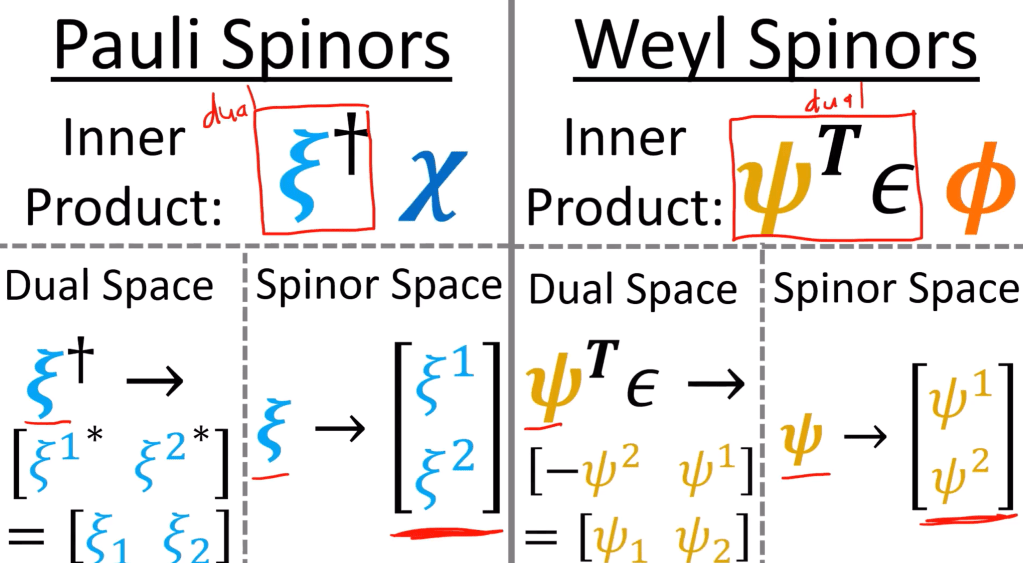
Pauli spinors don’t have chirality but Weyl spinors do, why

reference to https://www.youtube.com/watch?v=4NJBvkjpC3E&t=81s