A $k$-form assigns a (multi)linear, antisymmetric “density” to each point that can be evaluated on k tangent vectors. Density here is a bit abstract, but it  is not a “density” in the physics sense (mass per volume), but you can picture it as an oriented, multilinear measuring device that eats $k$k tangent vectors and spits out a number telling you “how much $k$k-dimensional stuff” they span at that point.

Let’s do concrete example on 1-form and 2-form to enhance the understanding

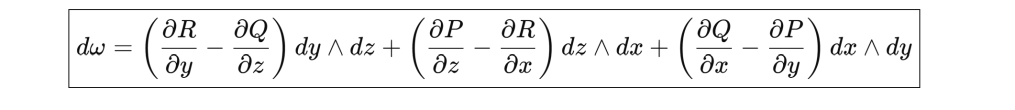
So what on earth is this “d”, exterior derivative” doing? It is measuring device, it measures infinitesimal circulation/flux density, or How much a quantity “flows around” or “spreads out” locally. It is the unified version of: divergence, gradient and curl. so F=dA means the EM field is the local circulation of the potential.

It leads to

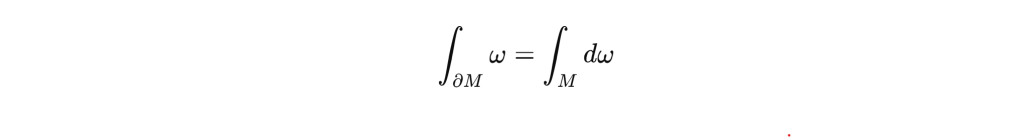
To fully grasp and appreciate the beauty of this Stoke’s theorem, we need to know what w and M is . M is manifold, ∂M is the surface/boundary of M, one dimension less. A or w here is the a flow field defined everywhere, if A is k-form, then dA is k+1 form.S

tokes’ theorem generalizes the fundamental theorem of calculus to higher dimensions: it says that integrating a derivative over a region can be reduced to integrating the original function over the boundary of that region.