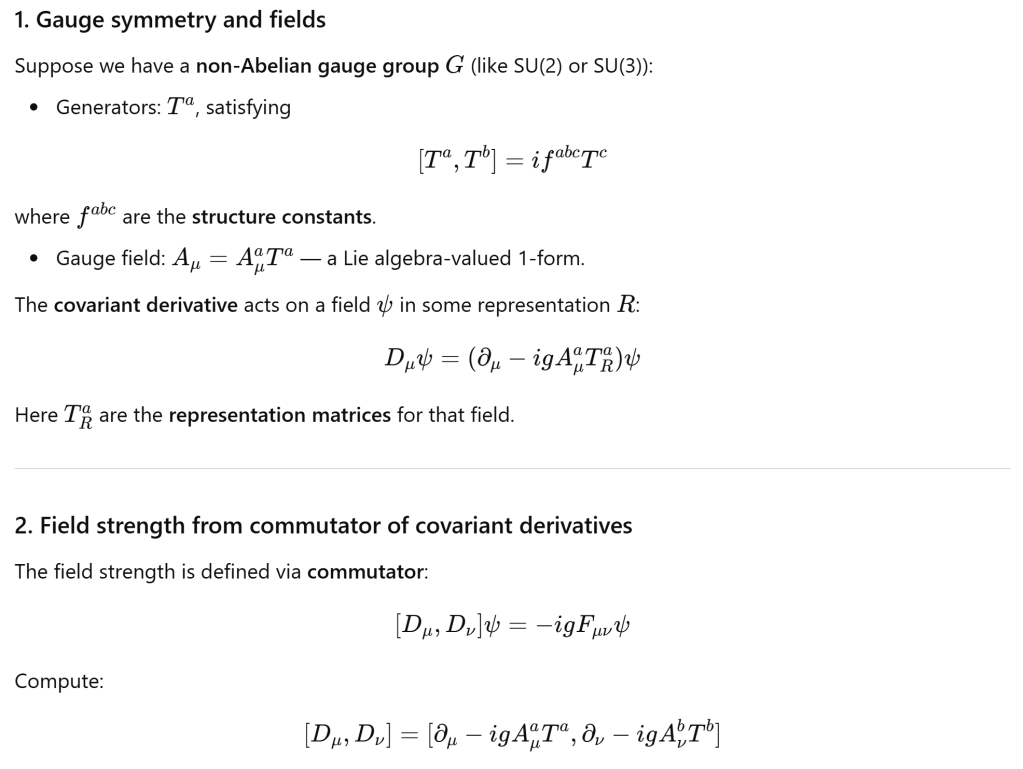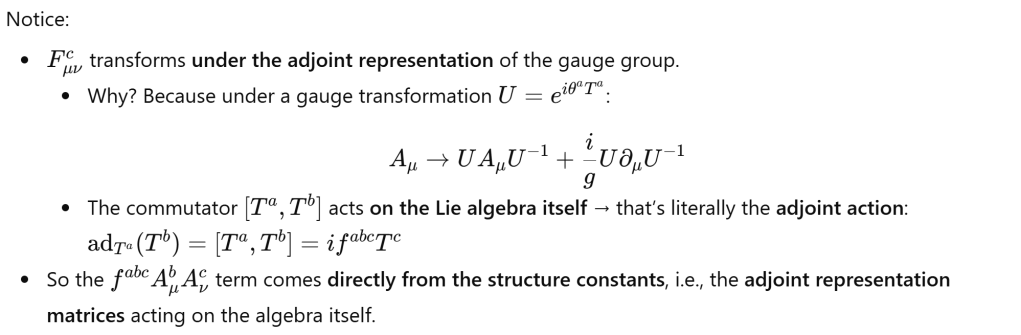Representation: Every group element is realized as a linear transformation on some vector space $V$, is a way to make an abstract symmetry concrete as matrices acting on vectors.

Use SU(2) as example,

So we have Trivial representation (spin 0), Fundamental representation (spin ½), Adjoint representation (spin 1) and Higher spin representations.

• In spin 0, the group does nothing.
• In spin 1/2, U∈SU(2), U acts on C2. this is called fundamental representation.
• In spin 1, the dimension is 2*1+1=3, AdU​(X)=UXU−1, this is called adjoint representation.

Tensor product gives a reducible representation. For SU(2), everything is built from trivial, fundamental and adjoint representations via tensor products.

Why representation is so important? Because Symmetry is fundamental. Representation theory tells us how symmetry manifests in the world.

First, let’s use representation theory to explain two electrons forming singlet and triplet states.

the math derivation is

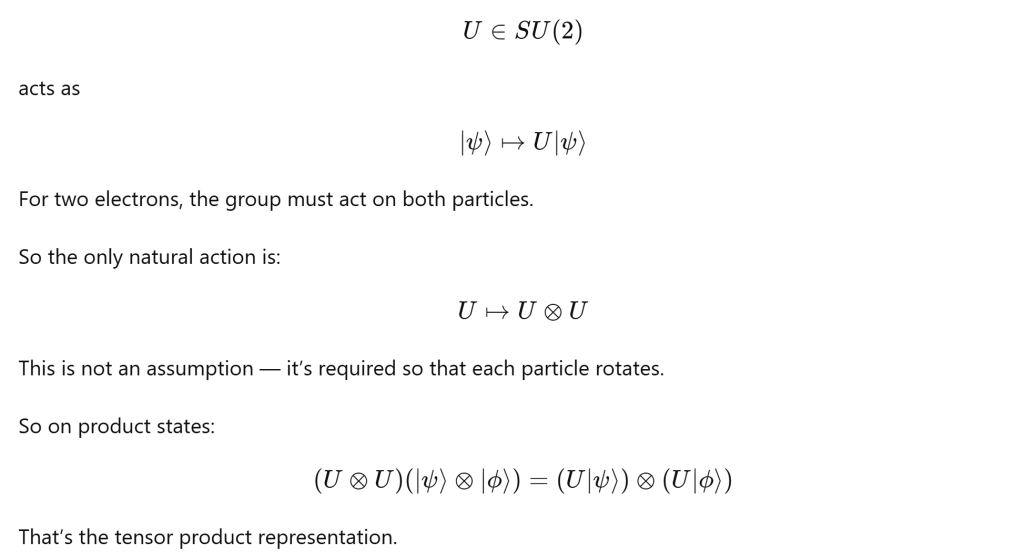
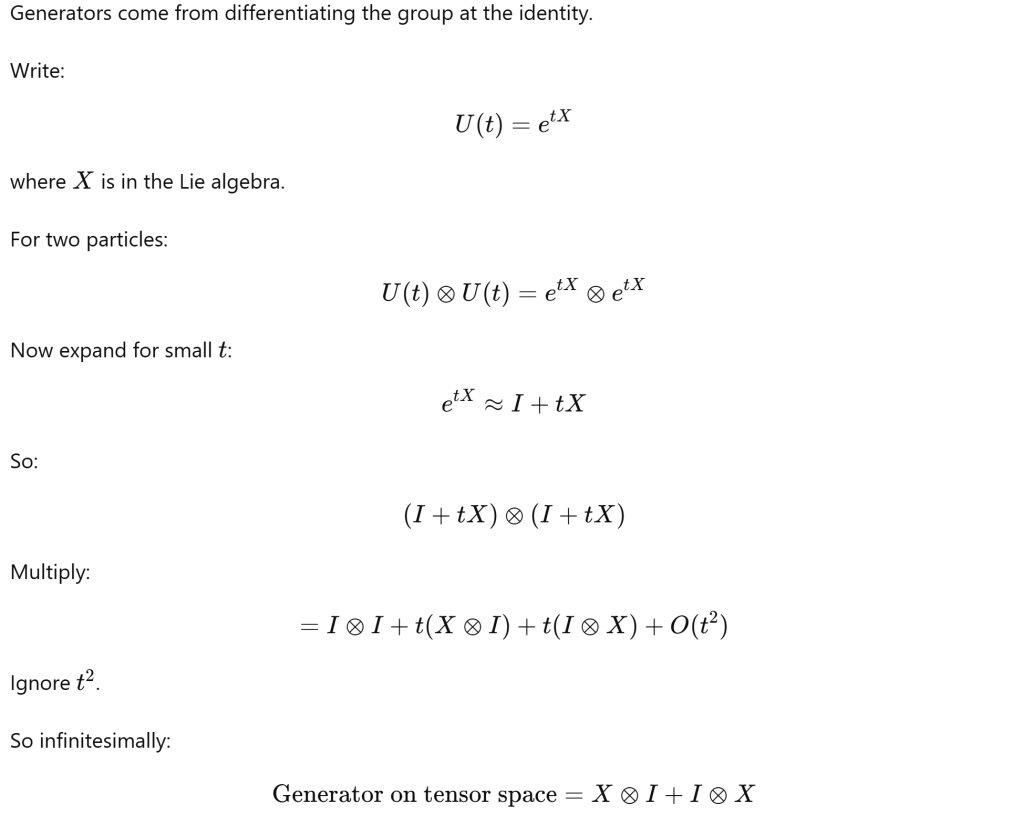
representation theory is the “language” that makes both the micro (electron spins) and macro (gauge fields, conservation laws) structures of physics understandable in a unified way. so

Second, let’s dive deeper to understand how adj representation play vital role at macro level to deduce gauge fields, conservation laws: