In last blog, we discussed the SU(2) representations:

Complexified Lorentz: SU(2)_L ⊕ SU(2)_R, We saw:$$\mathfrak{so}(1,3)_\mathbb{C} \cong \mathfrak{su}(2)_L \oplus \mathfrak{su}(2)_R$$so(1,3)C​≅su(2)L​⊕su(2)R​

So representations are tensor products:$$(j_L, j_R) = V_{j_L} \otimes V_{j_R}$$

Now let’s build a structured and precise picture of Lorentz representations,

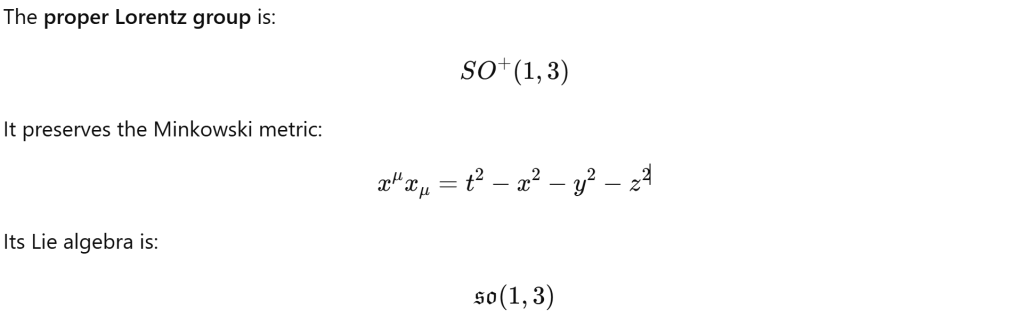
Math is the most beautiful and rigorous language, so we need to clarify when we say representation!

• A representation is a map from an algebra (or group) to linear operators on some vector space.
• The “vector space” itself (the space where the operators act) is sometimes loosely referred to as the representation, but strictly, the representation is the map + the space.

Example:

• SU(2) spin-1/2 representation = map from SU(2) generators → 2×2 Pauli matrices acting on $\mathbb{C}^2$C2
• The 2D space of spinors = “the representation space”

For the Lorentz group / algebra:

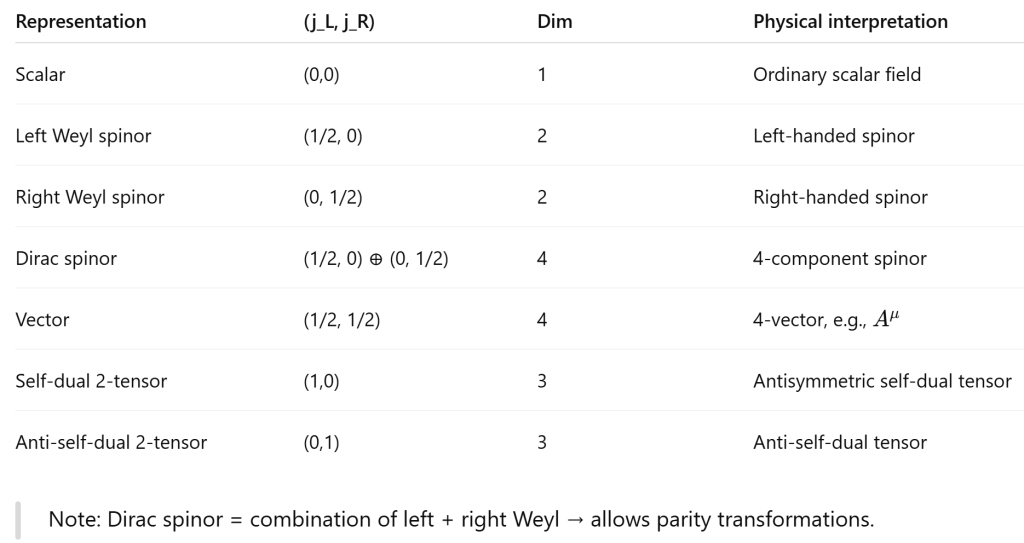
• Lorentz representation = any irreducible (or reducible) representation of $\mathfrak{so}(1,3)$so(1,3) (or the group $SO^+(1,3)$SO+(1,3)), so any of these in above table can be called a Lorentz representation, because they all carry an action of the Lorentz group.