Many times I was awed by some talented people solving convoluted problems in a clever cunning way, wondering how do they do it. Then, I realize if grasp the right methods and tools, I can solve lots of puzzles too.

I summarize the methods into the following kinds.

1. Break down to simple
2. Representation vividly by writing down or drawing a diagram
3. Representation by making or modeling things
4. Reversely deducing
5. Inferring
6. Self contradict
7. Thinking

1. Break down to simple – this technique is hugely used in solving all sorts of problems. For example, to calculate the turnover of a large portfolio, I start from a 2-stock portfolio and manually plug in stock price at each time point to get the sense of all intricacies might be embedded. Once 2-stock is straight clear, 3-stock, 10-stock, 1000-stock portfolio computation all follow the same rule.
2. Representation vividly by writing down or drawing a diagram – It’s futile to keep thinking and thinking without a slight effort to use aids. Drawing to writing down steps or painting/drawing is so powerful whereas people tend to ignore simply due to laziness. I found it greatly helpful to unclutter my mind by writing blogs or keep diaries. It is consistent with another statement (I forgot which famous person said so) that ‘language forms the way you think’. It’s damn right. So not only remember to write down our thoughts, in the process of writing down, we will recognize how inadequate we are in term of thinking ability, and it comes hand in hand with our inability to summon the right words or phrases to just express.
3. Representation by making or modeling things – it takes one step further from just writing down summaries or steps of approaching a problem, rather, this means we should just roll up the sleeves, do things, build models to figure out how to do it. I got great inspiration from watching Patrick Winston teaching Artificial Intelligence at MIT. On the very first class, he emphasized the importance of “representation” by bringing a wheel to the classroom. He asked the students which way the wheel will go if blown on a part of the wheel. He teased so-called “right-hand screw rule” that chemical engineers tend to solve this problem, instead, he took out a duck tape and stick onto the wheel and then deduce, then check by flipping it rolling. The video is here, pay attention at time 5:10. I also think the approach that Einstein tackles the greatest myth of time by imagining he is riding on the beam of light, or dwelling on an elevator going up or down is an adoption of representation method.
4. Reversely deducing – lots of complex math problems are solved in this way. For example, the lottery sequence problem, if the order of draw lottery affects the outcome or not? In this video, Yongle Li guided through the mathematical way to deduce the answer. If the rule of game changes as is illustrated in that second part of that video, the sequence of joining the game does matter. However, it would be diabolically difficult to jump to figure out a scenario of 5-people game, so, we start from two-people, then three-people, note, the three-people scenario calls forth 2-people variable to be plug-in. Note he took a very clever way to move A forward/after B, and hence assume a probability of P22 as if A becomes B.

• 5. Inferring – this technique is also vastly used in solving all sorts of problems. For example, we are asked to solve chicken rabbits problems since we are children. The question is that there are 15 heads and 40 legs in total, now you figure out how many are chicken, and how many are rabbits, given everybody knows a chicken has two legs, one head, a rabbit four legs, one head. We don’t have to lay out an algebra equation to calculate x, y value, instead, infer from heads/legs: if 15 heads, supposedly there are 15X4 = 60 legs if all rabbits, but in reality, only 40 legs are there, so additional 20 legs are from surplus legs of rabbits. for every one rabbit-chicken pair, there is two legs surplus, hence, a delta of 20 can be translated to 20/2 = 10 additional chicken, hence, the number of rabbits is 5. Problem is solved. The tricky part is to translate the delta as the additional number of chicken. Similarly, we can infer from the reverse direction:
  supposedly there are 15X2 = 30 legs if all chicken, now there are 40-30 =10 additional legs, these 10 legs have to be from rabbits, so the number of rabbits has to be 10/2 = 5. Another way to think reversely is to imagine the 40 legs subtracted by 15 heads twice, all chickens are gone, the rest (40-15-15 = 10) has to be 2-leg rabbits, hence the number of rabbits is 5. Assigning/interpreting a meaning for every math step is crucial to solving the problem
• 6. Self- contradicting – always ask and listen to opinions that are different than yourselves.
• 7. Thinking Aid – one quick example I come up with is in figuring out Monte Hall problem, imagine the rest of the two doors are merged into one, it’s much easier to further think after this simple trick/aid.

On Sep 2021, I want to add more on problem solving skills or framework, incorporating 3b1b’s summary.

What’s new in his version is to give things meaningful names, leverage symmetry and try describing one object via two different ways. For example to find if cos(theta)^2 = (1+cost(2theta))/2, a geometric diagram is drawn and instead of thinking of cos(theta)^2 as an area, he thinks of it as a ratio or length. so to connect to the right part.

Trial or guess is very important especially in solving complex ODE or PDE equations. That’s what those mathematicians use too.

Foremost importantly in my practice is to reduce to simple version, break down step by step in writing/drawing. For example in thinking the current weighting problem by Blackrock that they want to compare final weights to the liquidity adjusted weights, is it necessary to scale the liquid weight same as tier weight or is it trivial? How to approach it instead of resorting to gut feeling? Conjure up a simple extreme case: tier is composed to 1% and 99% liquidity weight, float adjusted weight is 25% and 25%, with another tier making the rest 50%. If everything scales same same pace, tier 1 should be 50% and 50%. If scale up 25% to say 45% and 45% in tier1, it’s closer to 50%, otherwise, it can be reduced to 5% and 5%, the multiples vary significantly…

Always follow steps, print out or write out each step is vital important in debugging. In capping algo, which is a recursive algo, I tend to forget return object twice, the first one returns itself, but additional return is necessary if the object needs to be assigned. Patiently run and print line by line is effective.

Finally, always to check, sanity checking by plugging in known cases adding up etc. Never skip this step.

As 3B1B pointed out, some people with perfect problem solving skills make you feel like they are genius, but they peruse and collecting, summarizing a lot so there is a wide web of connections in their brains already.

Adding again on Dec 08th, 2021, problem solving skills are honed and sometime I still were thrown off by wasting too much time unnecessary. A vital point I want to emphasize here is “details” or “sensitivity” or “observing really closely”!

For example, to find the projection of a vector x onto a directional vector v, the formula is hard to grasp:

Observe very closely, I found the first part the later part is not connected by a dot, instead, its expression is like elementary school way of expressing a scaler directly with a unit vector to express a scaled vector. However, the two magnitude/length of b is treated as if they are dotting/multiplying each other, hence equivalent to b dot b. This level of delicacy should be explicitly pointed out but never been clearly said by teachers.

Example 2, confusing question from beginners on Green’s theorem is always about “is gradient leading up to conservative vector field, or other way around”? grasping the concepts of gradient and conservative vector field, it’s not difficult to quickly deduce that gradient must be conservative, and if conservative, the vector should be written in a gradient format, that’s how the rule is deduced per Dr.Trefor’s video.

Observe closely can be accomplished by lay out the details in graph, written format. Also to write down and think deep of basic concepts. Don’t even try to skip steps or rush through, just ended up wasting more time.

Example3, conceptual problems such as inverse function theorem, implicit function theorem and Null space of a matrix(kernel).

Example 6, in calculating surface integral some tricks are applied, so causing confusion, if we observe/think closely of

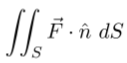
and

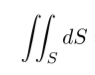
We know for latter – surface area computation, it can be the integral of tiny ru and rv cross product,

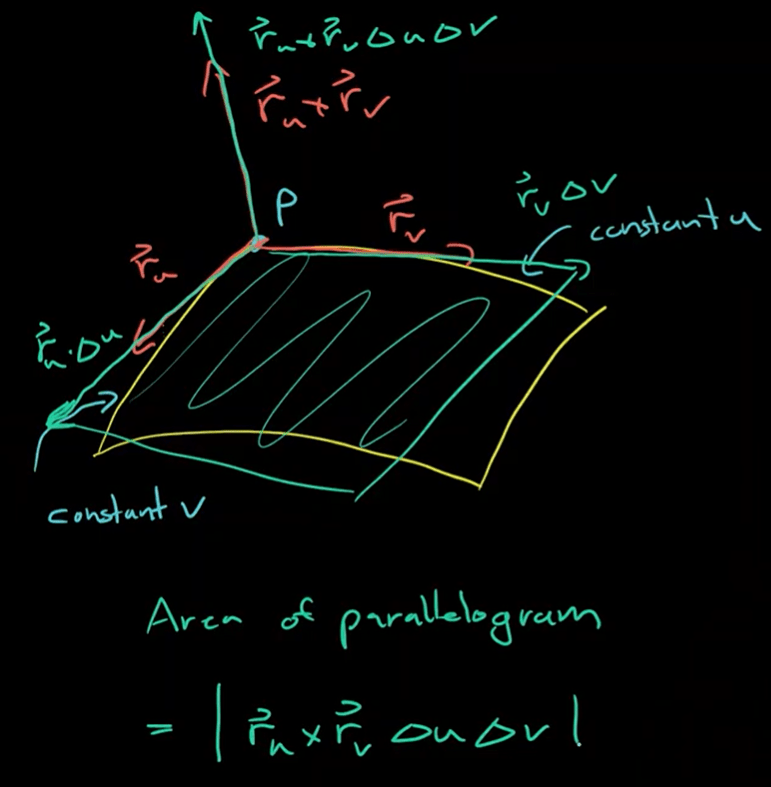
Now the question to ask is if this ru rv cross product a unit vector (unit normal) or just a vector (normal)? Observing/pondering through the above visual, it’s not too hard to deduce the cross product denotes both direction and length, so you can calculate the left part of Stoke Theorem directly. Observe/ponder deeper, you can deduce Green theorem is just the simpler version of Stoke Theorem.

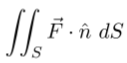
Next time if I spent too much time on something, force a stop, and try to write down, graph, look for concepts, and observe very very closely!