Knowing binomial distribution, especially that the E(x) = np and Variance of binomial distribution is P(1-P), we need to explore common multinomial scenario:

Let’s solve a real problem

Note the assumption of independency across these events is important. If this doesn’t hold,

Beta distribution seems like Bernoulli distribution, but it is to evaluate values in the range of [0, 1] instead of just two distinct values 0 or 1.

Plot beta distribution like

Note, gamma function is defined as

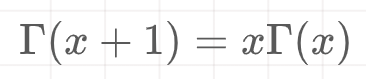
The Dirichlet distribution is a generalization of the beta distribution for multiple random variables. It is a distribution over distribution, in the same vein as Bayesian data analysis. The Dirichlet distribution is over vectors whose values are all in the interval [0, 1] and the sum of values in the vectors is 1. The K-dimensional Dirichlet distribution has a vector of parameters denoted alpha, given by

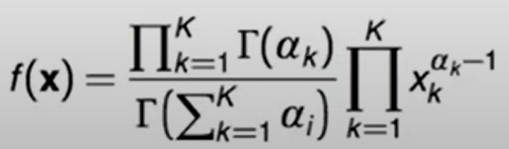
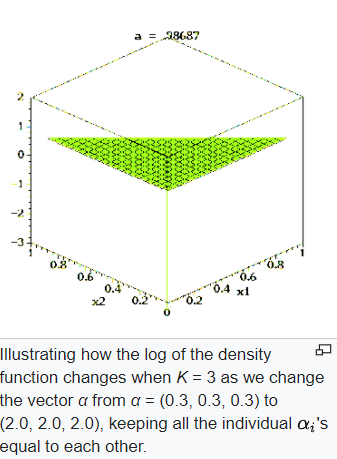
Just as the beta distribution is to binomial distribution, Dirichlet distribution is the same to the multinomial distribution. When we tie two distributions together, say multinomial distribution came from a Dirichlet distribution, perform Bayesian Data Analysis.