In QM, Born’s rule is a fundamental rule:

Leading to the definition of spinors either in light polarization expressed by Jones vector or Stern Gerlach experiment particles:

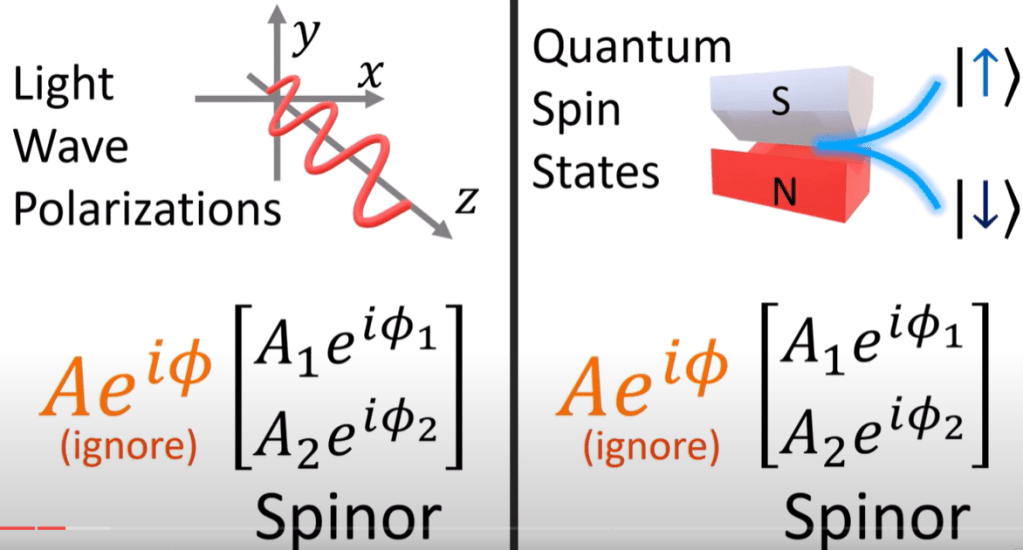
boiling down to only one complex number(two real number parameters) to consider in describing spinor, hence we use the bloch sphere,

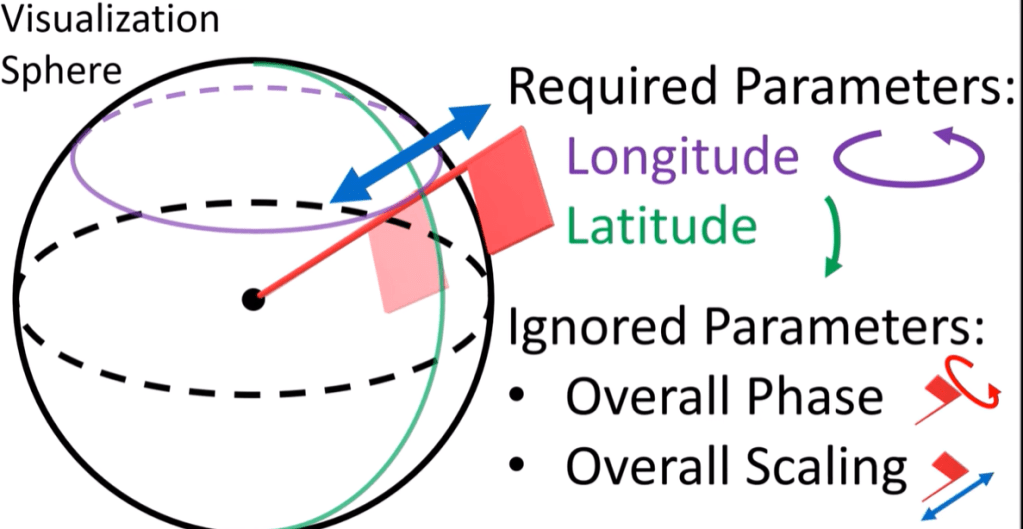
however, using the flagpole visualization we can view the full picture of the spinors. any sai can be written as the combination of two spinors as shown below, then manipulate to be

Once we saw this form, mathematically it’s consistent/identical to the CP1 (complex projective line), why?

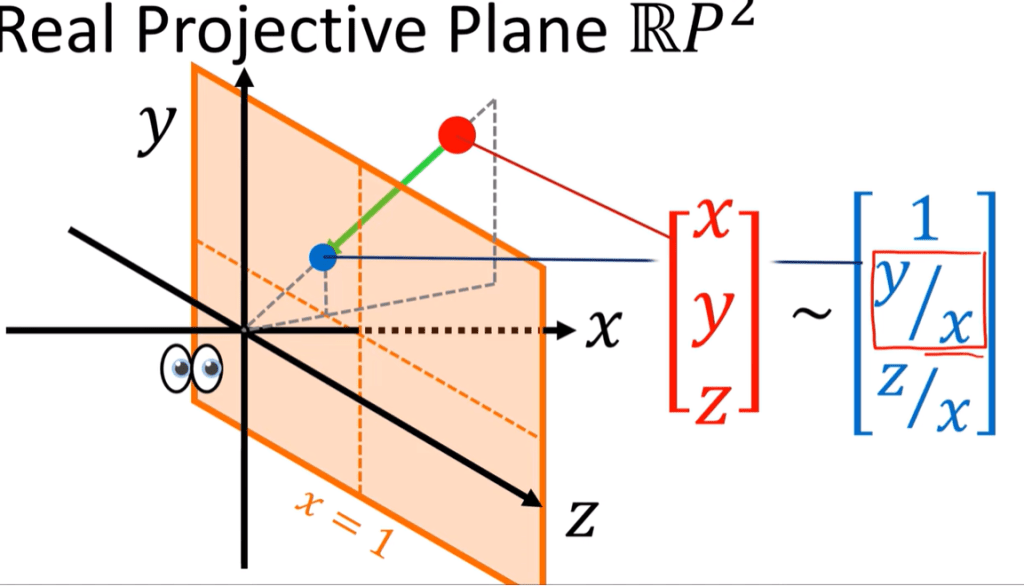
First, we need to know what is projection. there are orthogonal projection, perspective projection,

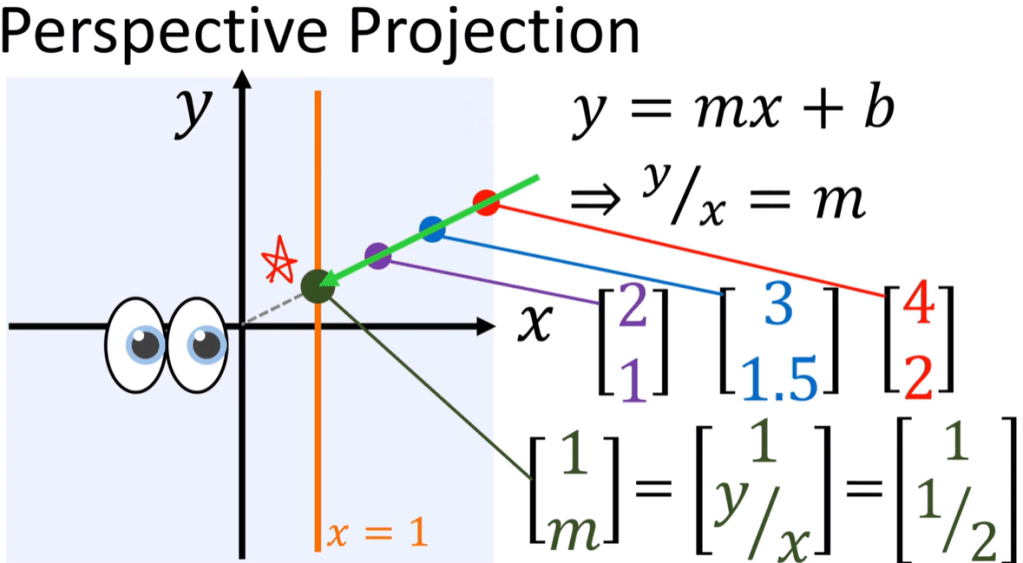
The line gets projected to is called real projective line CP1. Note the dots on the vertical line, i.e. the x component is 0, then the m value is infinite, we call those point on the vertical line – point at infinity.

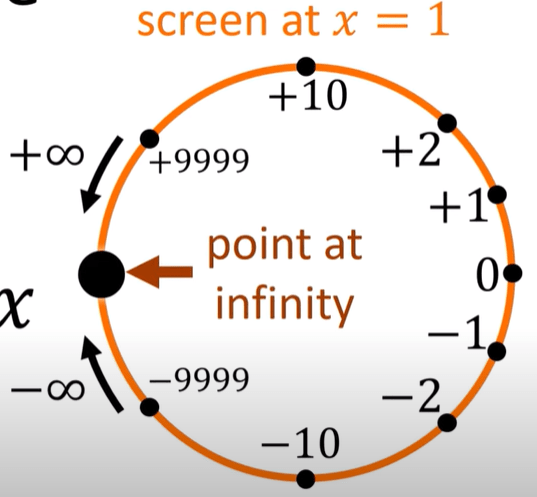
These points in high math is regarded as join together at positive and negative infinity.

Once grasp the concept of CP1/RP1, it’s easier to incrementally move to projective plane CP2/RP2, then goes higher dimensions.

The sphere has various names, once we touch on the projective geometry, it’s called from Poincare sphere to bloch sphere to now Riemann Sphere.

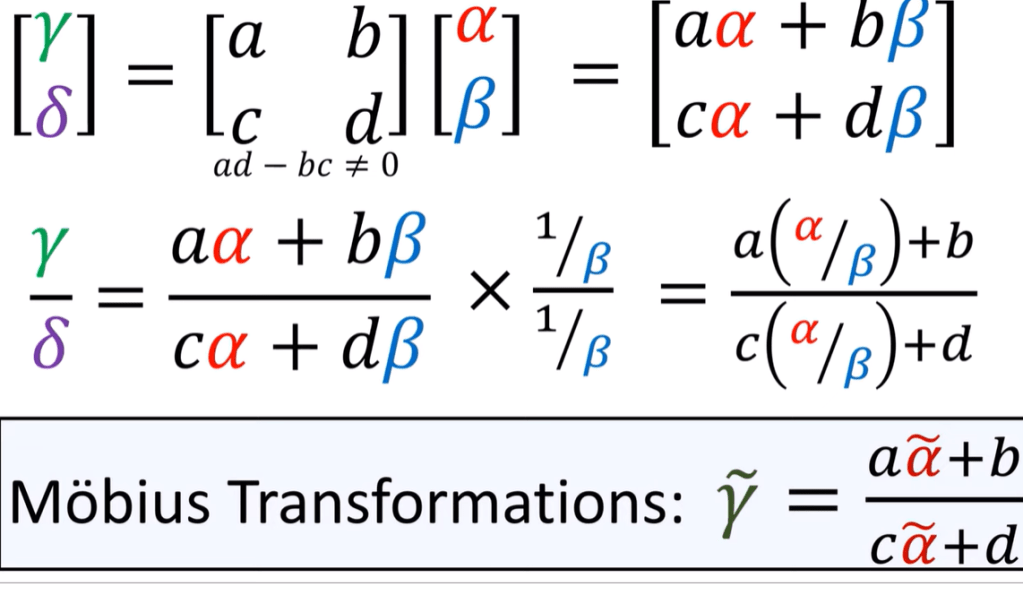
So now we know that spinor is a member of CP1.