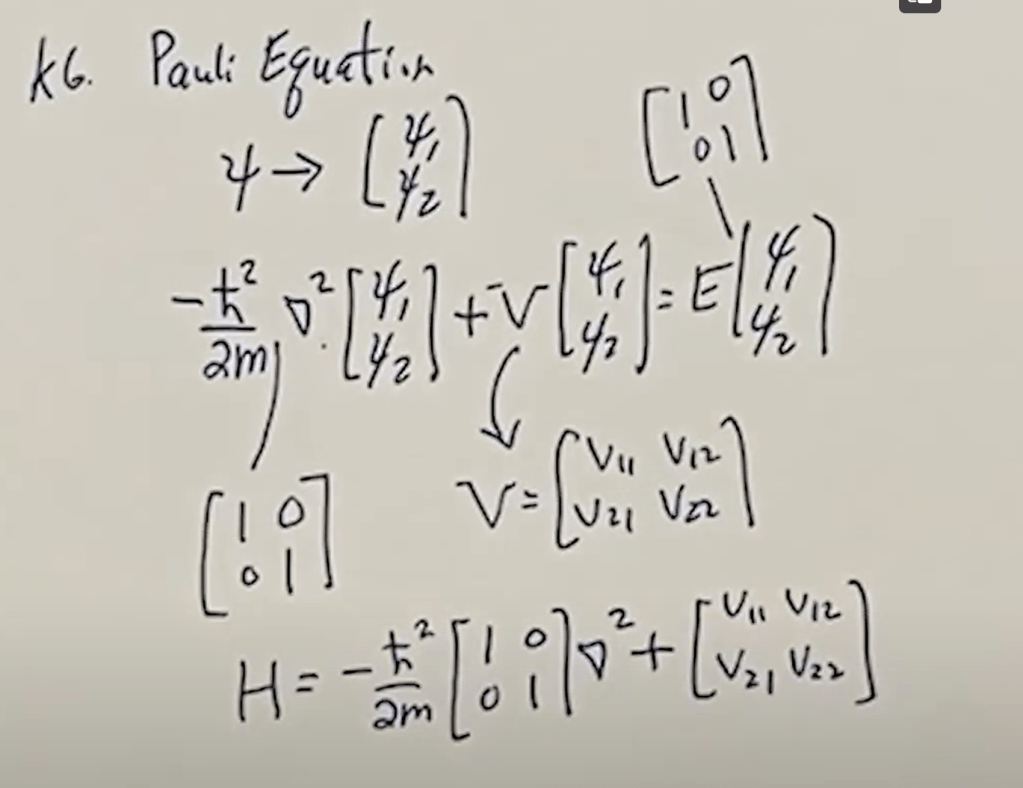Based on deep understanding of operator such as Halmiltonian to measure Energy (real value), we can apply a sigma z matrix on a quantum state such as below to get the eigen value – measurement too:

Note use sigma x to measure the state [1, 0], we can’t get [1, 0] back, instead, as detailed in previous blog, we know the eigen vector is 1/sqr2[1, -1] and 1/sqr2[1, 1], sigma x and sigma z are not simultaneous eigenvectors.

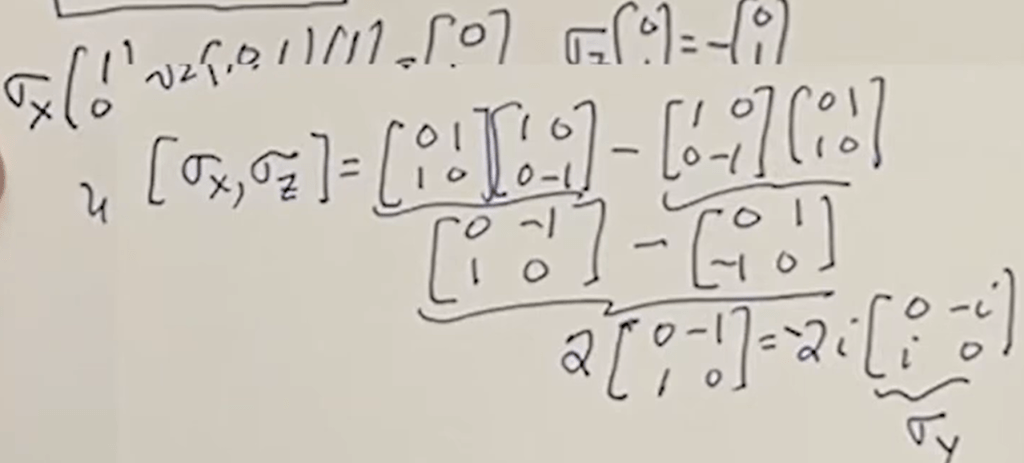
See how he deduce Heisenberg’s uncertainty principle:

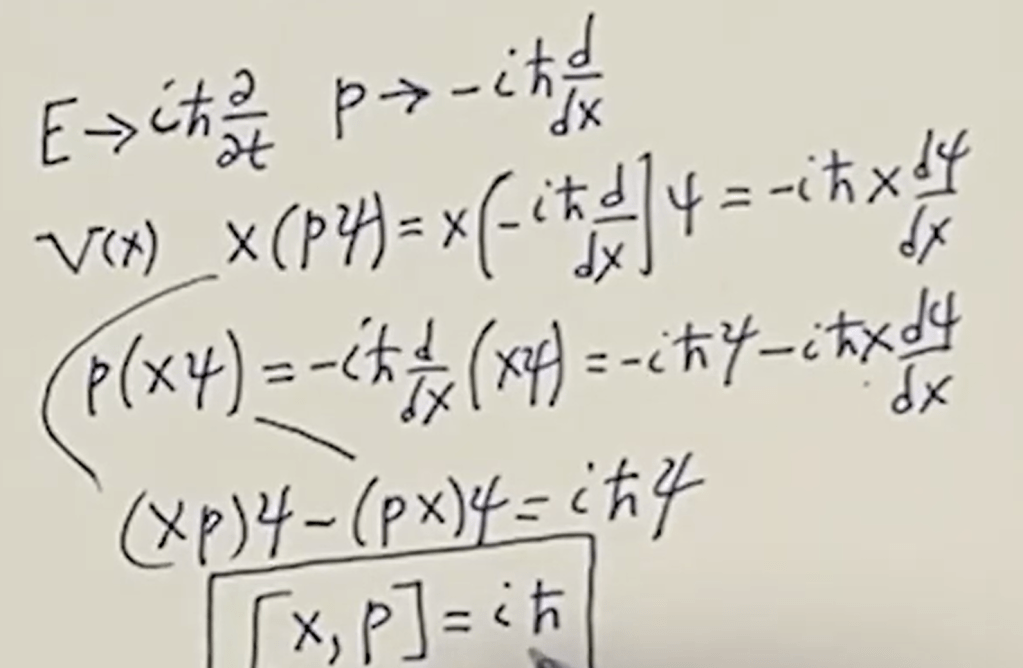
Then again, he solve the big puzzle that puzzled me for long time – how Max Born come up with the idea/conclusion that the sai function squared is the probability measurement?

Now to study angular momentum but plug in QM momentum operator:

A profound discovery that how similar looking the orbital angular momentum looks to Pauli matrices and the commutator properties! then after bit of math manipulation, and considering the dimensions both sides:

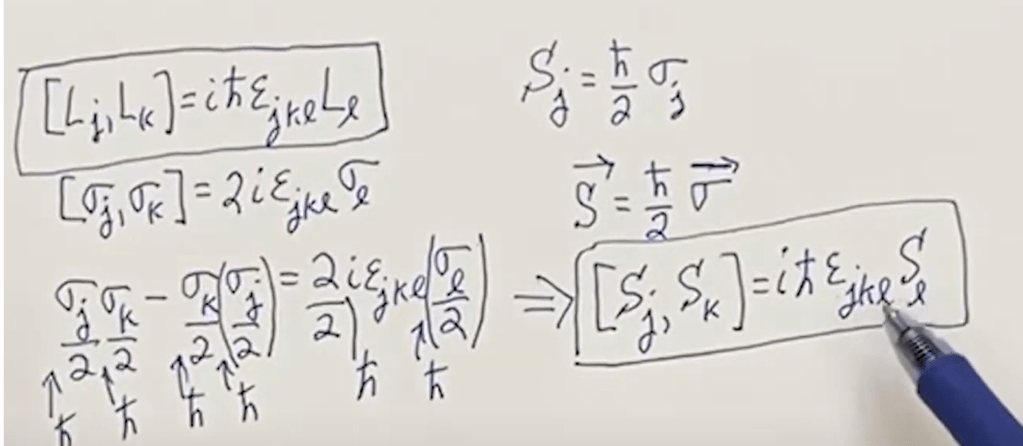
We define S, spinor that is exact form of orbital angular momentum! We call it Intrinsic angular momentum they have eigen states [1, 0] or [0, 1].

Omit the lengthy derivation, if we apply a unit normal vector dot product any sigma, then to find eigen value vector of this operator, we got the general form:

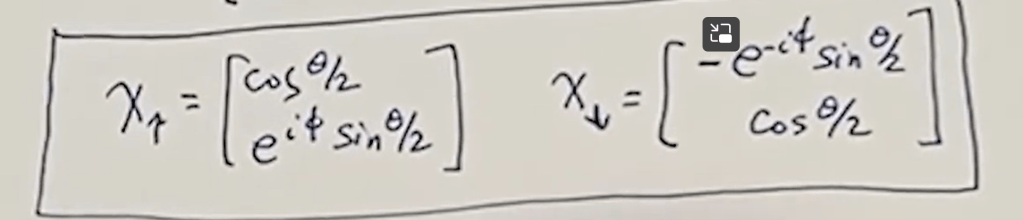
we can verify by recompute sigma z and eigen vector would reach [1, 0].

leading to the Pauli Equation