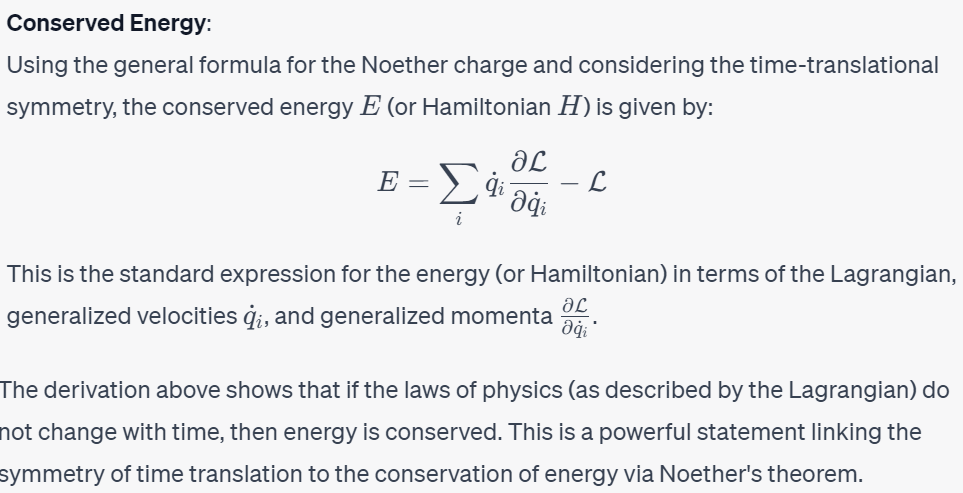Let’s derive Noether’s Conservation law given what we learned about Lagrangian.

When deriving a conservation law from a Lagrangian using Noether’s theorem, you introduce a small variation in the Lagrangian based on the symmetry you’re considering. After some manipulations, you’ll express the variation of the Lagrangian in terms of the equations of motion and another term. For the conservation law to hold, the term involving the equations of motion should be zero, which means the system must satisfy the equations of motion.

Now the generic form of Lagrangian

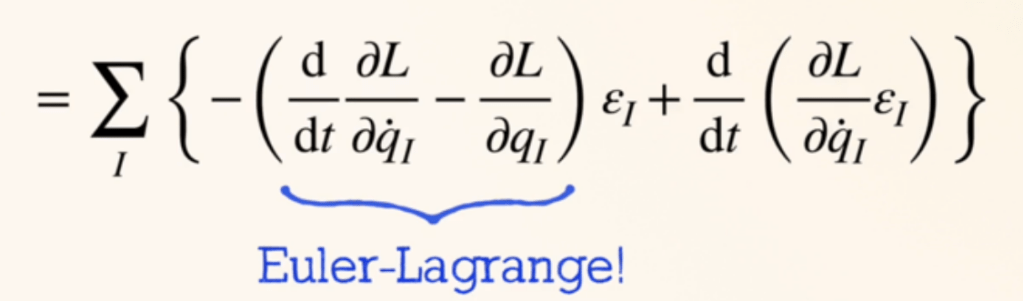
More generically, with infinitesimal transformations

what if we include or substract a time derivative of f in generic form above to make it more generic

f = La