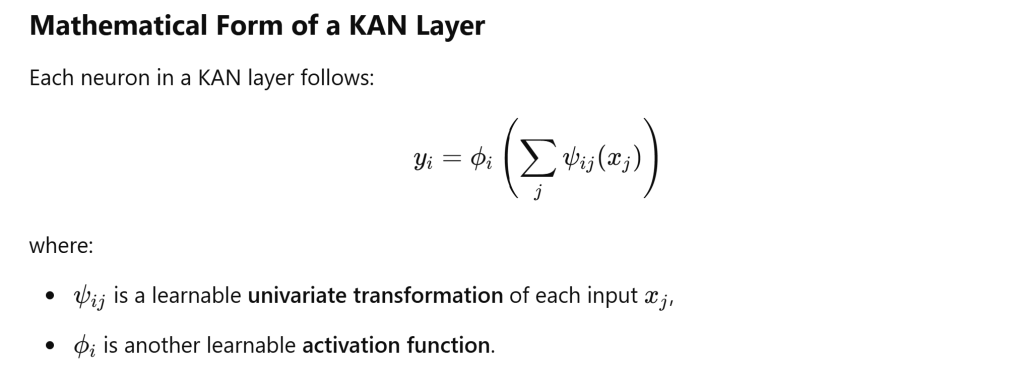
Kolmogorov-Arnold Networks (KANs) are a novel class of neural networks inspired by the Kolmogorov-Arnold Representation Theorem, which states that any multivariate function can be decomposed into a sum of univariate functions.

KANs differ from traditional neural networks by replacing weighted sum-based neurons with learnable, non-linear univariate functions. This allows them to have adaptive basis functions, making them more expressive and efficient compared to conventional architectures like MLPs (Multi-Layer Perceptrons).

It stems from Kolmogorov-Arnold Representation Theorem, which is quite like Fourier Series as both proved that any multivariate continuous function f(x1,x2,…,xn)f(x_1, x_2, …, x_n)f(x1​,x2​,…,xn​) can be represented as a sum of univariate functions.

The idea behind is quite similar to FEM numerical analysis, every function no matter how complex can be reduced to univariate functions represented by parameters.

We can compare KANs and MLPs

Feature	KANs	MLPs

Neuron Type

Learns functions ψ,ϕ\psi, \phiψ,ϕ

Weighted sum + activation

Expressivity

High (adapts basis functions)

Lower (fixed activation functions)

Training Efficiency

More efficient for some tasks

Requires more neurons/layers

Computational Cost

Can be lower (fewer parameters)

Higher (dense matrix multiplications)

Why Are KANs Exciting?

Adaptive & Efficient – Instead of using fixed activation functions, KANs learn the best transformation, leading to better generalization.
Fewer Parameters Needed – Since they use non-linear basis functions, they can approximate complex functions with smaller models.
Better Interpretability – Since the functions are explicit, they can be understood mathematically, unlike deep MLPs.

KANs are still a new area of research, but they could revolutionize AI architectures in physics-based modeling, scientific computing, and efficient deep learning.